Getaran Harmonik Sederhana dan Rumus dasarnya

Gerak Harmonik Sederhana

Gambar diatas merupakan salah satu aplikasi dari gerak harmonik sederhana

      Gerak Harmonik Sederhana adalah gerak bolak balik yang dialami suatu benda dari titik keseimbangan hingga titik pada jarak tertentu. Gerak Harmonik dibedakan menjadi dua macam, yaitu :

a. Gerak Harmonik pada Pegas.

b. Gerak Harmonik pada Bandul.

1. Gaya Pemulih

Gambar 1.1       

 Gaya Pemulih adalah gaya yang besarnya sama dengan gaya aksi, tetapi arahnya berlawanan. Perhatikan gambar 1.1! Susunan gaya pemulih pada pegas pada gambar 1.1 adalah C-B-A, apabila pegas digerakan dengan susunan A-B-C. Apabila pegas digerakan dengan susunan C-B-A, maka gaya pemulihnya A-B-C.

 Gambar 1.2

Perhatikan gambar 1.2! Secara matematis, gaya pemulih dapat dirumuskan sebagai berikut.

Fp = - k . ∆x

Fp = Gaya pemulih , satuannya N.

k = konsanta pegas, satuannya N/m.

∆x = simpangan pegas, satuannya m.

Gambar 1.3

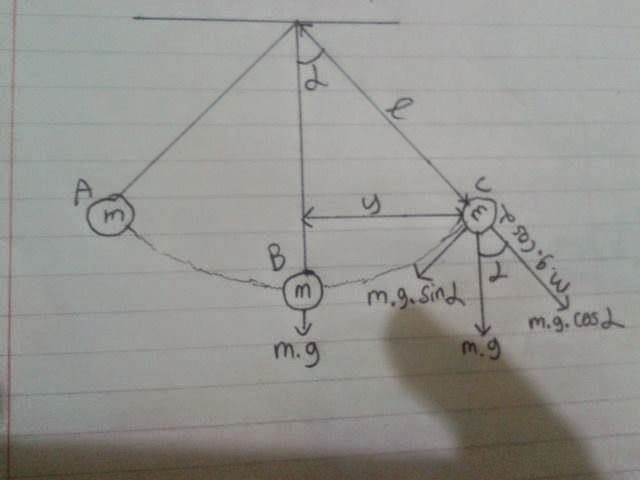
Perhatikan Gambar 1.3! Susunan gaya pemulih pada bandul tersebut jika susunan gaya simpangannya A-B-C adalah C-B-A. Sedangkan jika susunan arah gaya simpangannya C-B-A, maka susunan gaya pemulihnya adalah A-B-C.

Gambar 1.4

Perhatikan Gambar 1.4! Secara matematis, gaya pemulih pada bandul dirumuskan pada gambar 1.5. Perhatikan gambar 1.5!

  

Gambar 1.5

2. Persamaan Gerak Harmonik Sederhana

• Percepatan GHS. Percepatam GHS dirumuskan pada gambar 1.6. Perhatikan gambar 1.6!

          Gambar 1.6

• Tetapan pegas. Tetapan pegas dirumuskan pada gambar 1.7. Perhatikan gambar 1.7!

         Gambar 1.7
        

• Periode dan frekuensi pada pegas. Frekuensi dan periode dirumuskan pada gambar 1.8. Perhatikan gambar 1.8!

          Gambar 1.8

• Simpangan. Simpangan dirumuskan pada gambar 1.9. Perhatikan gambar 1.9!

Gambar 1.9

• Kecepatan GHS. Rumus kecepatan GHS merupakan turunan dari rumus simpangan. Kecepatan GHS dirumuskan pada gambar 1.10. Perhatikan gambar 1.10!

Gambar 1.10

•  Percepatan GHS. Rumus percepatan GHS merupakan turunan dari rumus kecepatan GHS. Percepatan GHS dirumuskan pada gambar 1.11. Perhatikan gambar 1.11!

Gambar 1.11

• Periode dan frekuensi pada bandul. Periode dan frekuensi pada bandul dirumuskan pada gambar 1.12. Perhatikan gambar 1.12!

Gambar 1.12

       
       
           

•  Fase dan sudut fase. Fase disebut keadaan suatu benda yang dilihat dari arah simpangan dan getarnya. Fase dirumuskan pada gambar 1.13! Perhatikan gambar 1.13!

          Gambar 1.13

             Sudut fase dirumuskan pada gambar 1.14! Perhatikan gambar 1.14!
Gambar 1.14

 






             Apabila fase dan sudut fase diperhitungkan, maka persamaan umum GHS dirumuskan pada gambar 1.15. Perhatikan gambar 1.15!
Gambar 1.15

•   Energi pada GHS

           a. Energi Potensial. Energi potensial dirumuskan pada gambar 1.16. Perhatikan gambar 1.16!
               

               Gambar 1.16

Perhatikan! Rumus diatas mengunakan rumus integral.

            Perhatikan gambar 1.17!  Pada gambar 1.17, dijelaskan bahwa rumus Ep dipadukan dengan rumus simpangan, sehingga menjadi sebagai berikut. Lihat gambar 1.17. (∆x = y )

 
 

                    Gambar 1.17

b. Energi kinetik. Energi kinetik dirumuskan pada gambar   1.18. Perhatikan gambar 1.18!                          Gambar 1.18                             c. Energi mekanik. Energi mekanik dirumuskan pada gambar 1.19. Perhatikan gambar 1.19!                 Gambar 1.19